区分的定数分布とは，定義域を複数の区分（区間，セル，ビンなど）に分割し，それぞれの区分内で確率密度関数が一定値を取るように定義された確率分布である．
このような分布は，解析的に扱いにくい密度関数を近似したり，モンテカルロ法・重要度サンプリングで効率的にサンプリングしたりするために広く利用される．
import gc
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec
# from mpl_toolkits.axes_grid1 import make_axes_locatable
import numpy.typing as npt
from typing import TypeAlias, overload
# from typing import overload
rng = np.random.default_rng(12345)
# print(plt.style.available)
plt.style.use("seaborn-v0_8")区間 \([0,1]\) を \(\Delta=\frac{1}{N}\) で分割し，端点 \(x_{i}=i\Delta\quad(i=0,\dots,N)\) とする．
\[ f(x)= \begin{cases} v_{0} \quad x_{0}\le x\lt x_{1}\\ v_{1} \quad x_{1}\le x\lt x_{2}\\ \vdots\\ v_{N-1} \quad x_{N-1}\le x\lt x_{N}\\ \end{cases} \]
積分は，
\[ c =\int_{0}^{1} f(x)\,dx =\sum_{i=0}^{N-1} \int_{x_{i}}^{x_{i+1}} f(x)\,dx =\sum_{i=0}^{N-1}v_{i}\Delta =\sum_{i=0}^{N-1}\frac{v_{i}}{N} \]
確率密度関数は，
\[ p(x)=\frac{f(x)}{c} \]
累積分布関数は区分的に線形な関数となり，その値は各点 \(x_{i}\) において次のように定義される．
\[ \begin{align*} P(x_{0})&=0\\ P(x_{i}) &=\int_{x_{0}}^{x_{i}} p(x)\,dx =\int_{x_{0}}^{x_{i-1}} p(x)\,dx+\int_{x_{i-1}}^{x_{i}} p(x)\,dx\\ &=P(x_{i-1})+\frac{v_{i-1}}{cN} ,\quad(i=1,\dots,N) \end{align*} \]
\([x_{i},x_{i+1})\) では，累積分布関数は傾き \(v_{i}/c\) で線形に増加する．累積分布関数は単調増加なので，任意の \(\zeta\) に対し \(x\) の値は必ず \([x_{i},x_{i+1})\) に存在し，
\[ P(x_{i})\le\zeta\lt P(x_{i+1}) \]
が成り立つ．累積分布関数の値の配列が与えられていれば，このような \(P(x_{i})\) の組は二分探索によって効率的に求めることができる．よって逆関数法によるサンプリングでは，対応する区間が決まれば \(x\) の値は次のように与えられる．
\[ x=\left(i+\frac{\zeta-P(x_{i})}{P(x_{i+1})-P(x_{i})}\right)\Delta \]
class Distribution1D:
def __init__(self, f: npt.NDArray[np.floating], *, dtype: npt.DTypeLike = np.float32) -> None:
self.dtype = np.dtype(dtype)
self.func = np.asarray(f, dtype=self.dtype)
n = len(self.func)
# Compute integral of step function at x_i
self.cdf = np.zeros(n + 1, dtype=self.dtype)
self.cdf[1:] = np.cumsum(self.func / n, axis=0)
# Transform step function integral into CDF
self.func_int = self.cdf[n]
if self.func_int == self.dtype.type(0):
self.cdf = np.linspace(0, 1, n + 1, dtype=self.dtype)
else:
self.cdf /= self.func_int
def count(self) -> int:
return len(self.func)
@overload
def sample_continuous(self, u: float | np.floating) -> tuple[np.floating, np.floating, np.int32]: ...
@overload
def sample_continuous(self, u: npt.NDArray[np.floating]) -> tuple[npt.NDArray[np.floating], npt.NDArray[np.floating], npt.NDArray[np.int32]]: ...
def sample_continuous(self, u):
u = np.asarray(u, dtype=self.dtype)
# Find surrounding CDF segments and offset
offset = np.searchsorted(self.cdf, u, side="right") - 1
offset = np.clip(offset, 0, len(self.cdf) - 2).astype(np.int32)
# Compute offset along CDF segment
du = u - self.cdf[offset]
seg = self.cdf[offset + 1] - self.cdf[offset]
du = np.where(seg > self.dtype.type(0), du / seg, du)
# Compute PDF for sampled offset
x = (offset.astype(self.dtype) + du) / self.count()
pdf = self.func[offset] / self.func_int
# Return x in [0,1) corresponding to sample
if np.ndim(u) == 0:
return x[()], pdf[()], offset[()]
return x, pdf, offset
@overload
def sample_discrete(self, u: float | np.floating) -> tuple[np.int32, np.floating, np.floating]: ...
@overload
def sample_discrete(self, u: npt.NDArray[np.floating]) -> tuple[npt.NDArray[np.int32], npt.NDArray[np.floating], npt.NDArray[np.floating]]: ...
def sample_discrete(self, u):
u = np.asarray(u, dtype=self.dtype)
# Find surrounding CDF segments and offset
offset = np.searchsorted(self.cdf, u, side="right") - 1
offset = np.clip(offset, 0, len(self.cdf) - 2).astype(np.int32)
pdf = self.func[offset] / (self.func_int * self.count())
u_remapped = (u - self.cdf[offset]) / (self.cdf[offset + 1] - self.cdf[offset])
if np.ndim(u) == 0:
return offset[()], pdf[()], u_remapped[()]
return offset, pdf, u_remapped
@overload
def discrete_pdf(self, index: int | np.integer) -> np.floating: ...
@overload
def discrete_pdf(self, index: npt.NDArray[np.integer]) -> npt.NDArray[np.floating]: ...
def discrete_pdf(self, index):
return self.func[index] / (self.func_int * self.count())def histogram_1d(sampler, sample_size, batch_size, rng, bins, range=None):
dtype = sampler(1, rng).dtype
if isinstance(bins, int):
edges = np.linspace(*range, bins + 1, dtype=dtype)
else:
edges = np.asarray(bins, dtype=dtype)
H_total = np.zeros(len(edges) - 1, dtype=np.int64)
remaining = sample_size
while remaining > 0:
current_batch = min(batch_size, remaining)
samples = sampler(current_batch, rng)
H_batch, _ = np.histogram(samples, bins=edges, range=range, density=False)
H_total += H_batch
remaining -= current_batch
del samples, H_batch
gc.collect()
H_density = H_total / (sample_size * np.diff(edges))
return H_density, edges
def plot_distribution_1d(distr: Distribution1D, sample_size: int, rng: np.random.Generator) -> None:
n = distr.count()
x = np.linspace(0, 1, n + 1, dtype=distr.dtype)
indices = np.arange(distr.count())
def continuous_sampler(sample_size: int, rng: np.random.Generator):
return distr.sample_continuous(rng.random(sample_size, dtype=distr.dtype))[0]
def discrete_sampler(sample_size: int, rng: np.random.Generator):
return distr.sample_discrete(rng.random(sample_size, dtype=distr.dtype))[0]
data = [
{"title": "Input function f", "ylabel": "f(x)", "plot_fn": lambda ax: ax.step(x[:-1], distr.func, where="post", linewidth=1)},
{"title": "CDF", "ylabel": "CDF(x)", "plot_fn": lambda ax: ax.step(x, distr.cdf, where="post", linewidth=1)},
{
"title": f"Cont. PDF (N={sample_size})",
"ylabel": "Density",
"legend": True,
"data_fn": lambda: (
histogram_1d(continuous_sampler, sample_size, 100000, rng, bins=x),
distr.func[indices] / distr.func_int,
),
"plot_fn": lambda ax, hist_data, pdf: (
ax.bar(hist_data[1][:-1], hist_data[0], width=np.diff(hist_data[1]), align="edge", alpha=0.6, label="sample histogram"),
ax.step(hist_data[1][:-1], pdf, where="post", color="red", linestyle="--", linewidth=1, alpha=0.6, label="Theoretical PDF"),
),
},
{
"title": f"Disc. PMF (N={sample_size})",
"ylabel": "Probability",
"legend": True,
"data_fn": lambda: (
histogram_1d(discrete_sampler, sample_size, 100000, rng, bins=np.arange(distr.count() + 1)),
distr.discrete_pdf(indices),
),
"plot_fn": lambda ax, hist_data, pdf: (
ax.bar(hist_data[1][:-1], hist_data[0], width=np.diff(hist_data[1]), align="edge", alpha=0.6, label="sample histogram"),
ax.step(hist_data[1][:-1], pdf, where="post", color="red", linestyle="--", linewidth=1, alpha=0.6, label="Theoretical PMF"),
),
},
]
nrows_ncols = (1, len(data))
base_w, base_h = plt.rcParams.get("figure.figsize")
figsize = (base_w * nrows_ncols[1], base_h * nrows_ncols[0])
subplot_kw = {"xlabel": "x"}
fig, axs = plt.subplots(nrows=nrows_ncols[0], ncols=nrows_ncols[1], subplot_kw=subplot_kw, figsize=figsize)
axs = np.atleast_1d(axs).flatten()
for ax, datum in zip(axs, data):
res = ()
if "data_fn" in datum:
res = datum["data_fn"]() # type: ignore
datum["plot_fn"](ax, *res) # type: ignore
ax.set_title(datum["title"])
ax.set_ylabel(datum["ylabel"])
ax.grid(True)
if datum.get("legend"):
ax.legend()def gaussian1d(x, x0, sigma):
return np.exp(-((x - x0) ** 2) / (2 * sigma**2))
x = np.linspace(0, 1, 64 + 1)
peaks_1d = [(0.25, 0.03, 0.8), (0.55, 0.05, 0.3), (0.8, 0.02, 0.9)]
f = sum(a * gaussian1d(x, x0, s) for x0, s, a in peaks_1d)
f = f[:-1].astype(np.float32)
plot_distribution_1d(Distribution1D(f), 500 * f.size, rng)
２次元関数 \(f(u,v)\) が，\(u_{i}\in[0,1,\dots,n_{u}-1],\,v_{j}\in[0,1,\dots,n_{v}-1]\) に対して \(f[u_{i},v_{j}]\) の値によって定義され，\(f[u_{i},v_{j}]\) は範囲 \([\frac{i}{n_{u}},\frac{i+1}{n_{u}})\times[\frac{j}{n_{v}},\frac{j+1}{n_{v}})\) で一定の値を取るとする．連続値 \((u,v)\) が与えられたとき，対応する離散インデクス \((\tilde{u},\tilde{v})\) を \(\tilde{u}=\lfloor n_{u}u\rfloor,\,\tilde{v}=\lfloor n_{v}v\rfloor\) と定義し，\(f(u,v)=f[\tilde{u},\tilde{v}]\) とする．
\(f\) の積分は \(f[u_{i},v_{j}]\) の値の単純な和になる．
\[ I_{f} =\iint_{[0,1]^{2}} f(u,v)\,dudv =\sum_{i=0}^{n_{u}-1}\sum_{j=0}^{n_{v}-1}\int_{\frac{i}{n_{u}}}^{\frac{i+1}{n_{u}}}\int_{\frac{j}{n_{v}}}^{\frac{j+1}{n_{v}}} f[u_{i},v_{j}]\,dvdu\\ =\frac{1}{n_{u}n_{v}}\sum_{i=0}^{n_{u}-1}\sum_{j=0}^{n_{v}-1} f[u_{i},v_{j}] \]
\(f\) の同時確率密度関数は，
\[ p(u,v) =\frac{f(u,v)}{I_{f}} =\frac{f[\tilde{u},\tilde{v}]}{\frac{1}{n_{u}n_{v}}\sum_{i=0}^{n_{u}-1}\sum_{j=0}^{n_{v}-1} f[u_{i},v_{j}]} \]
周辺確率密度関数は，\(f[u_{i},v_{j}]\) の値の和として計算できる．
\[ p(v) =\int_{0}^{1} p(u,v)\,du =\frac{1}{I_{f}}\int_{0}^{1} f(u,v)\,du =\frac{\frac{1}{n_{u}}\sum_{i=0}^{n_{u}-1} f[u_{i},\tilde{v}]}{I_{f}} \]
この関数は，\(\tilde{v}\) にのみ依存するため，\(n_{v}\) 個の値で定義される区分的定数１次元関数 \(p[\tilde{v}]\) となる．\(v\) のサンプルが与えられたとき，条件付き確率密度関数は，
\[ p(u|v) =\frac{p(u,v)}{p(v)} =\frac{\frac{f[\tilde{u},\tilde{v}]}{I_{f}}}{p[\tilde{v}]} =\frac{f[\tilde{u},\tilde{v}]}{\frac{1}{n_{u}}\sum_{i=0}^{n_{u}-1} f[u_{i},\tilde{v}]} \]
特定の \(\tilde{v}\) の値が与えられたとき，\(p[\tilde{u}|\tilde{v}]\) は \(\tilde{u}\) の区分的定数１次関数であり，通常の１次元手法でサンプリングが可能である．\(\tilde{v}\) の各値に対して \(n_{v}\) 個の異なる１次元条件付き密度が存在する．
class Distribution1DBatch:
def __init__(self, funcs: npt.NDArray[np.floating], *, dtype: npt.DTypeLike = np.float32):
# funcs: shape (M, N) (M distributions, each length N)
self.dtype = np.dtype(dtype)
self.func = np.asarray(funcs, dtype=self.dtype)
M, N = self.func.shape
# Compute integral of step function at x_i
self.cdf = np.zeros((M, N + 1), dtype=self.dtype)
self.cdf[:, 1:] = np.cumsum(self.func / N, axis=1)
# Transform step function integral into CDF
self.func_int = self.cdf[:, -1].copy()
mask = self.func_int == self.dtype.type(0)
self.cdf[mask] = np.linspace(0, 1, N + 1, dtype=self.dtype)
mask = ~mask
self.cdf[mask] /= self.func_int[mask, None]
def sample_continuous(self, u: npt.NDArray[np.floating], batch_idx: npt.NDArray[np.integer]) -> tuple[npt.NDArray[np.floating], npt.NDArray[np.floating], npt.NDArray[np.int32]]:
u = np.asarray(u, dtype=self.dtype)
rows = batch_idx
cdf_rows = self.cdf[rows]
_, N = self.func.shape
# Find surrounding CDF segments and offset
cols = (cdf_rows[:, 1:] <= u[:, None]).sum(axis=1) # vectorized searchsorted
cols = np.clip(cols, 0, N - 1, dtype=np.int32)
# Compute offset along CDF segment
row_idx = np.arange(len(u))
du = u - cdf_rows[row_idx, cols]
seg = cdf_rows[row_idx, cols + 1] - cdf_rows[row_idx, cols]
du = np.where(seg > self.dtype.type(0), du / seg, du)
# Return x in [0,1) corresponding to sample
x = (cols.astype(self.dtype) + du) / N
pdf = self.func[rows, cols] / self.func_int[rows]
return x, pdf, cols
class Distribution2D:
def __init__(self, func: npt.NDArray[np.floating], *, dtype: npt.DTypeLike = np.float32) -> None:
self.dtype = np.dtype(dtype)
nv, nu = func.shape
# Compute conditional sampling distribution for v_tilde
self.conditional_v = Distribution1DBatch(func, dtype=self.dtype)
# Compute marginal sampling distribution p[v_tilde]
marginal_func = self.conditional_v.func_int
self.marginal = Distribution1D(marginal_func, dtype=self.dtype)
def sample_continuous(self, u):
u = np.asarray(u, dtype=self.dtype)
is_single = u.ndim == 1
u = np.atleast_2d(u)
d1, pdf1, v = self.marginal.sample_continuous(u[:, 1])
d0, pdf0, _ = self.conditional_v.sample_continuous(u[:, 0], v)
x = np.stack([d0, d1], axis=-1)
pdf = pdf0 * pdf1
if is_single:
return np.squeeze(x, axis=0), np.squeeze(pdf, axis=0)[()]
return x, pdf
def pdf(self, p):
p = np.asarray(p, dtype=self.dtype)
is_single = p.ndim == 1
p = np.atleast_2d(p)
nv, nu = self.conditional_v.func.shape
iu = np.clip((p[:, 0] * nu).astype(np.int32), 0, nu - 1)
iv = np.clip((p[:, 1] * nv).astype(np.int32), 0, nv - 1)
pdf = self.conditional_v.func[iv, iu] / self.marginal.func_int
if is_single:
return np.squeeze(pdf, axis=0)[()]
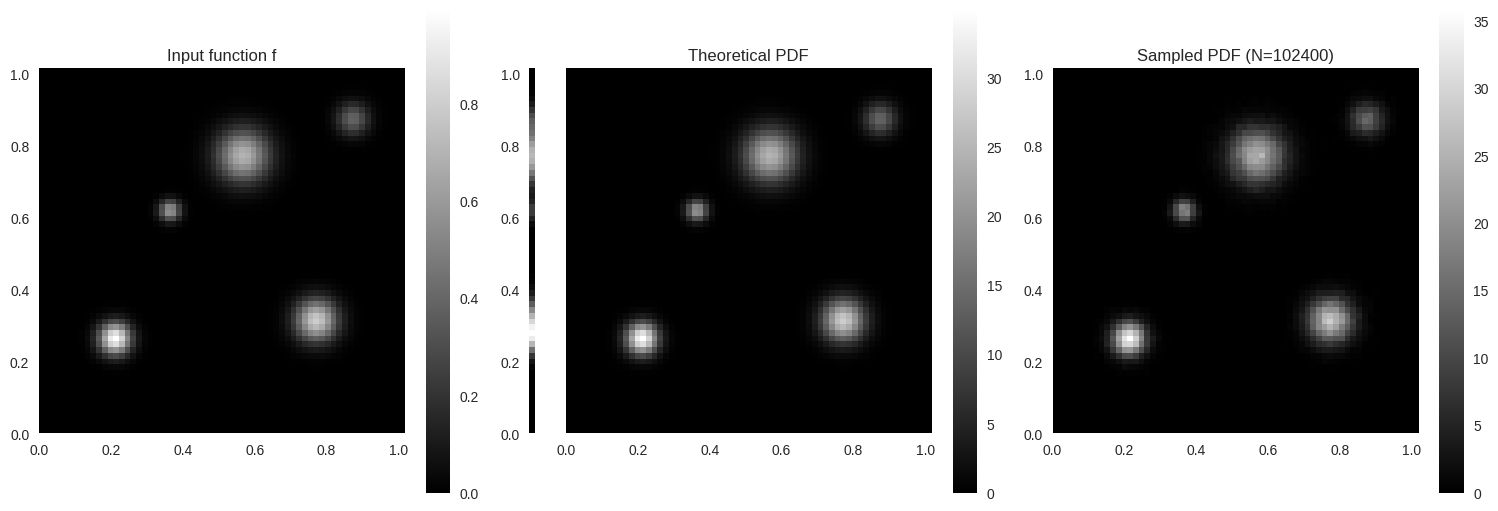
return pdfdef histogram_2d(sampler, sample_size, batch_size, rng, bins, range=None):
dtype = sampler(1, rng).dtype
if isinstance(bins, int):
xedges = np.linspace(*range, bins + 1, dtype=dtype)
yedges = np.linspace(*range, bins + 1, dtype=dtype)
elif isinstance(bins[0], int) and isinstance(bins[1], int):
xedges = np.linspace(*range[0], bins[0] + 1, dtype=dtype)
yedges = np.linspace(*range[1], bins[1] + 1, dtype=dtype)
else:
xedges = np.asarray(bins[0])
yedges = np.asarray(bins[1])
H_total = np.zeros((len(xedges) - 1, len(yedges) - 1))
remaining = sample_size
while remaining > 0:
current_batch = min(batch_size, remaining)
samples = sampler(current_batch, rng)
H_batch, _, _ = np.histogram2d(samples[:, 0], samples[:, 1], bins=(xedges, yedges), range=range, density=False)
H_total += H_batch
remaining -= current_batch
del samples, H_batch
gc.collect()
area = np.diff(xedges)[:, None] * np.diff(yedges)[None, :]
H_density = H_total / (sample_size * area)
return H_density, xedges, yedges
def plot_distribution_2d(distr: Distribution2D, sample_size: int, rng: np.random.Generator) -> None:
def gen_marginal_pdf():
indices = np.arange(distr.marginal.count())
pdf = distr.marginal.func[indices] / distr.marginal.func_int
return pdf[:, None]
def gen_pdf():
nv, nu = distr.conditional_v.func.shape
u = np.linspace(0, 1, nu + 1, dtype=distr.dtype)[:-1]
v = np.linspace(0, 1, nv + 1, dtype=distr.dtype)[:-1]
U, V = np.meshgrid(u, v)
points = np.stack([U.ravel(), V.ravel()], axis=-1)
return distr.pdf(points).reshape(nv, nu)
def gen_histogram():
sampler = lambda sample_size, rng: distr.sample_continuous(rng.random((sample_size, 2), dtype=distr.dtype))[0]
H, _, _ = histogram_2d(sampler, sample_size, 100000, rng, bins=(nu, nv), range=((0, 1), (0, 1)))
return H.T
nv, nu = distr.conditional_v.func.shape
data = [
{"title": "Input function f", "data_fn": lambda: distr.conditional_v.func, "width": nu},
{"title": "", "hide_cbar": True, "hide_xticks": True, "data_fn": gen_marginal_pdf, "width": 1},
{"title": "Theoretical PDF", "hide_yticks": True, "sharey_with": 1, "data_fn": gen_pdf, "width": nu},
{"title": f"Sampled PDF (N={sample_size})", "data_fn": gen_histogram, "width": nu},
]
aspect_ratio = nv / nu
subplot_width = 5
subplot_height = subplot_width * aspect_ratio
figsize = (subplot_width * (len(data) - 1), subplot_height)
fig = plt.figure(figsize=figsize, constrained_layout=True)
fig.set_constrained_layout_pads(w_pad=0.1)
gs = gridspec.GridSpec(1, len(data), figure=fig, width_ratios=[datum["width"] for datum in data])
axs = [fig.add_subplot(gs[i]) for i in range(len(data))]
xticks = np.linspace(0, nu - 1, 6)
xticklabels = [f"{x:.1f}" for x in np.linspace(0, 1, 6)]
yticks = np.linspace(0, nv - 1, 6)
yticklabels = [f"{y:.1f}" for y in np.linspace(0, 1, 6)]
for ax, datum in zip(axs, data):
X = datum["data_fn"]() # type: ignore
ny, nx = X.shape
im = ax.imshow(X, cmap="gray", aspect="equal", interpolation="nearest", extent=[0, nx, 0, ny])
ax.set_title(datum["title"])
ax.set_xticks(xticks)
ax.set_xticklabels(xticklabels)
ax.set_yticks(yticks)
ax.set_yticklabels(yticklabels)
ax.set_xlim(0, nx)
ax.set_ylim(0, ny)
ax.grid(False)
if datum.get("hide_xticks"):
ax.tick_params(axis="x", which="both", bottom=False, labelbottom=False)
if datum.get("hide_yticks"):
ax.tick_params(axis="y", which="both", left=False, labelleft=False)
if "sharey_with" in datum:
ax.sharey(axs[datum["sharey_with"]])
cbar = fig.colorbar(im, ax=ax)
cbar.ax.set_visible(not datum.get("hide_cbar", False))
plt.show()def gaussian2d(x, y, x0, y0, sigma):
return np.exp(-((x - x0) ** 2 + (y - y0) ** 2) / (2 * sigma**2))
nu, nv = 64, 64
u_edges = np.linspace(0, 1, nu + 1)[:-1]
v_edges = np.linspace(0, 1, nv + 1)[:-1]
U, V = np.meshgrid(u_edges, v_edges)
peaks_2d = [
(0.20, 0.25, 0.03, 1.0),
(0.75, 0.30, 0.04, 0.8),
(0.55, 0.75, 0.05, 0.7),
(0.35, 0.60, 0.02, 0.6),
(0.85, 0.85, 0.03, 0.4),
]
f = sum(a * gaussian2d(U, V, u0, v0, s) for u0, v0, s, a in peaks_2d)
f = f[::-1]
f = f.astype(np.float32)
plot_distribution_2d(Distribution2D(f), 25 * f.size, rng)
球面上の方向 \(\omega\) を選ぶ確率は，その方向の輝度 \(L(\omega)\) に比例すると考えられる．微小な立体角要素 \(d\omega\) を用いると，
\[ p_{\Omega}(\omega)\,d\omega \propto L(\omega)\,d\omega \]
と書ける．立体角要素は，
\[ d\omega =\sin\theta\,d\theta d\phi \]
であるため，球面座標では，
\[ p_{\Theta,\Phi}(\theta,\phi)\,d\theta d\phi \propto L(\theta,\phi)\sin\theta\,d\theta d\phi \]
となる．環境マップの画像座標 \((u,v)\) を，
\[ u=\frac{\phi}{2\pi} \,\quad v=\frac{\theta}{\pi} \]
とすると，ヤコビアンより，
\[ d\theta d\phi =\left|\frac{\partial(\theta,\phi)}{\partial(u,v)}\right|\,dudv =2\pi^{2}\,dudv \]
が得られる．これを代入すると，
\[ p_{\Theta,\Phi}(\theta,\phi)\,d\theta d\phi \propto L(\theta,\phi)\sin\theta (2\pi^{2}\,dudv) \]
すなわち，
\[ p_{U,V}(u,v)\,dudv \propto L(u,v)\sin(\pi v) (2\pi^{2}\,dudv) \]
となる．比例定数は正規化により相殺されるため，
\[ p_{U,V}(u,v) \propto L(u,v)\sin(\pi v) \]
を得る．
from PIL import Image
import requests
from io import BytesIO
def load_image_from_url(url):
response = requests.get(url)
response.raise_for_status()
img = Image.open(BytesIO(response.content))
return img
img = load_image_from_url("https://www.pbr-book.org/3ed-2018/Monte_Carlo_Integration/hdr-env-orig.png")img_np = np.array(img.convert("RGB"), dtype=np.float32) / 255.0
height, width, _ = img_np.shape
coeff = np.array([0.2126, 0.7152, 0.0722], dtype=img_np.dtype)
luminance = np.dot(img_np, coeff)
v = np.arange(height)
sin_theta = np.sin(np.pi * (v + 0.5) / height)
luminance *= sin_theta[:, None]plot_distribution_2d(Distribution2D(luminance), 25 * luminance.size, rng)